[Transformer Series]- Positional Encoding Notes

What is Positional Encoding?

Positional encoding is one of the most crucial yet often overlooked components that make modern transformer models work effectively. While transformers have revolutionized natural language processing and beyond, they face a fundamental challenge: unlike recurrent neural networks that process sequences step by step, transformers process all tokens in parallel, losing the inherent understanding of word order.

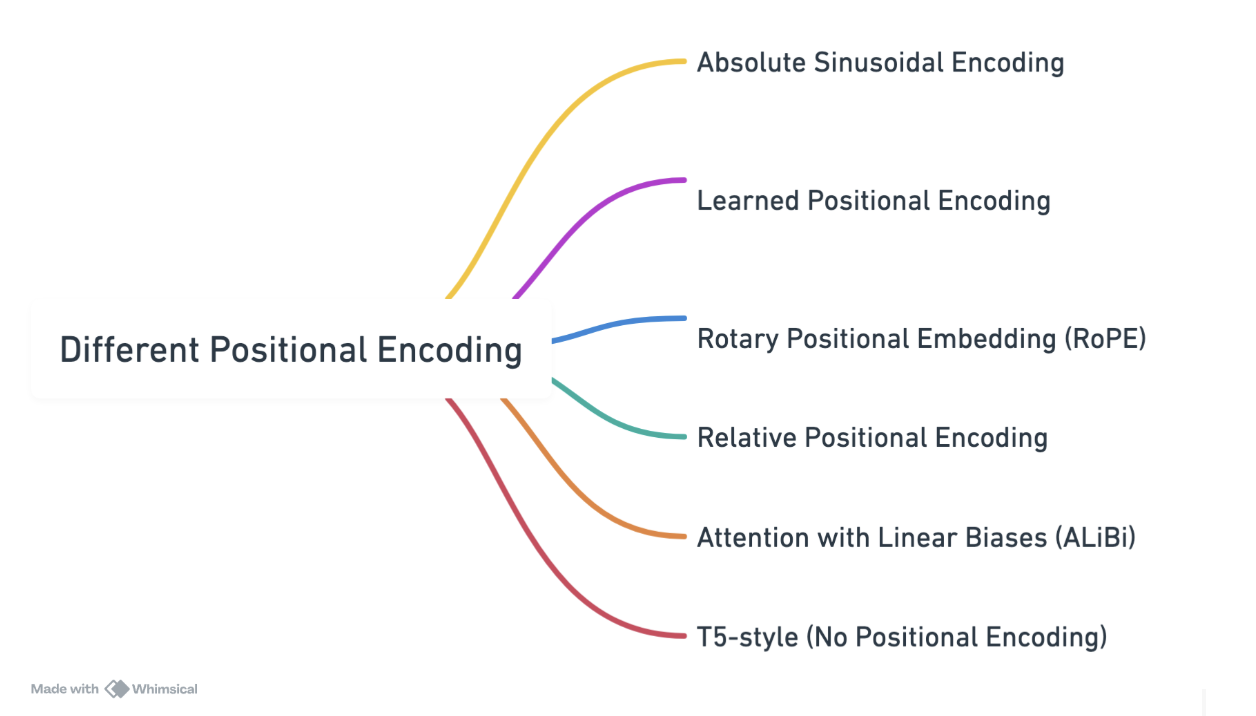
Different Kind of Positional Encoding

Positional Encoders

Abosulte Positional Encoding

Mathematical Representation of Abosulte Positional Encoding

For even dimension:

PE_{(pos, 2i)} = \sin\left(\frac{pos}{10000^{\frac{2i}{d_{model}}}}\right)

For odd dimension:

PE_{(pos, 2i+1)} = \cos\left(\frac{pos}{10000^{\frac{2i}{d_{model}}}}\right)

Code

import numpy as np 

import matplotlib.pyplot as plt 

  

# create the positional encoding function using the formula above 

def getPositionEncoding(seq_len, d, n=10000): 

    # instantiate an array of 0s as a starting point 
    P = np.zeros((seq_len, d)) 
    # iterate through the positions of each word  
    for k in range(seq_len): 
        #calculate the positional encoding for even and odd position of each word 
        for i in np.arange(int(d/2)): 
            denominator = np.power(n, 2*i/d) 
            P[k, 2*i] = np.sin(k/denominator) 
            P[k, 2*i+1] = np.cos(k/denominator) 
    return P